Branching Off a Route at Angle θ

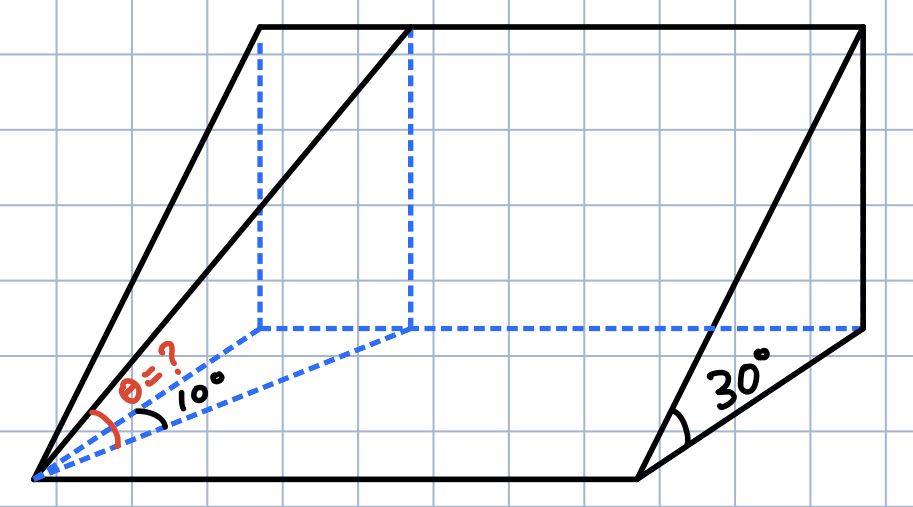
Consider the following question:

You are climbing a mountain by the steepest route at a slope of 30° when you come upon a trail branching off at a 10° angle from yours. What is the angle of ascent of the branch trail?

When the question says you are climbing up a route which is inclined at an angle of 30° it is fairly straightforward, the angle between the ground and the slope is 30° in angle.

Now we look at the branching off part of the question. It says a trail branches off from the route at an angle of 10°.

There are two possible options here that comes to your mind, hopefully:

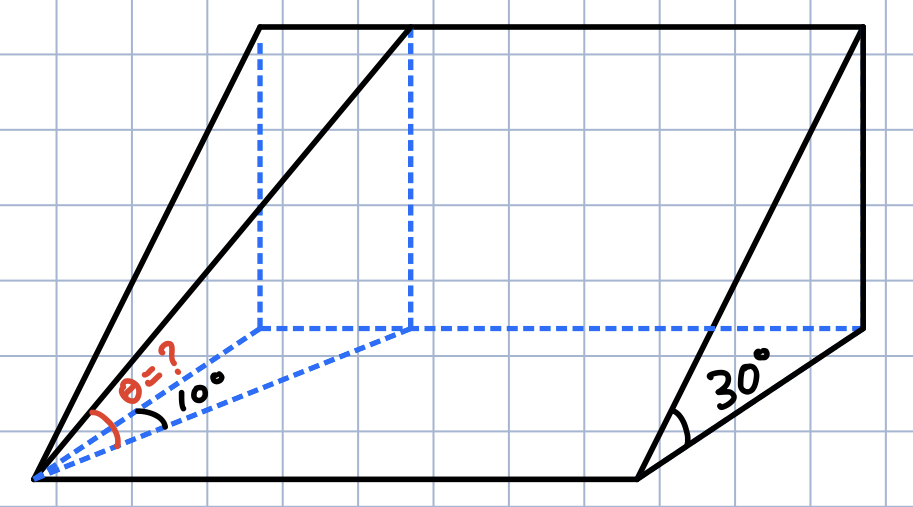
1. The projection of the path which branches off from the original route forms a 10° angle with the projection of the original route
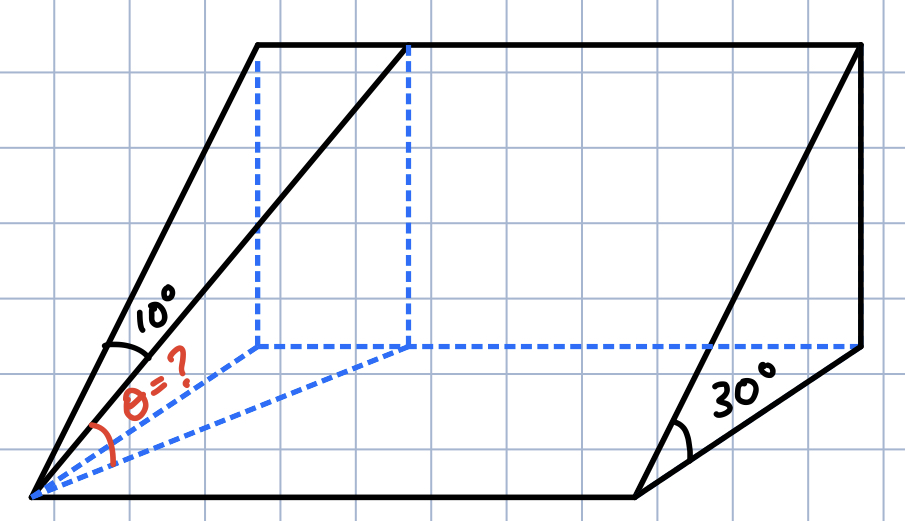
2. The path that branches off forms a 10° angle with the original route on the 30° inclined surface

With either of these two assumptions, you are supposed to find the angle between the branched route and the ground.

To put the two possible assumptions into perspective, we can put them into a frame in 3 dimensions.

(1) would yield this:

(2) would yield this:

These two all seem like possibilities...

BUT

what do you think when you are actually walking on a path?

You're definitely not going to model a projection onto the flat ground and make that projection deviate 30° from the projection of the route you are currently on.

Instead, what you see in front of you is: the path, the angle between the branch and the path. And not the angle in the other case.

After some calculations, you get the following solutions:

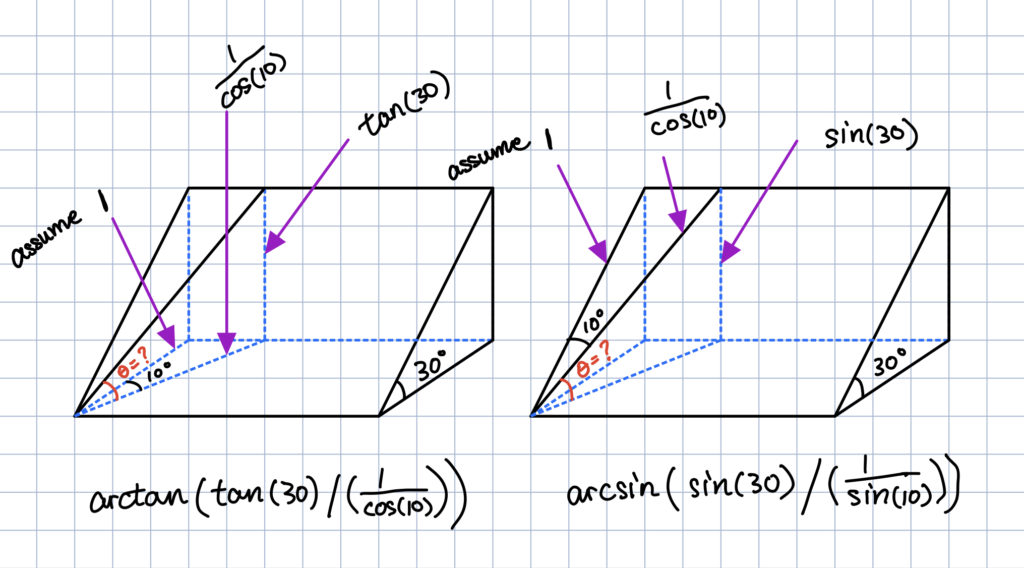
Now, we can put the interpretation that makes sense into the grading website

And you get...

0 Points

Congrats!!...

But wait, I did it perfectly?! How is it wrong?!

Now a thought pops into your mind... What if, out of some possibility that the question is saying the other case...

So you re-calculated and put the the answer...

1 Point

So it turns out that the answer that makes less sense is the correct answer...

Which is not how you would normally think of it:

If this question were to be on a test, you would've thought you got the perfect answer, and be wrong, happily.

Some problems nowadays just aren't created perfectly, there are made from a concept(which is the only way, I admit), but they never truly consider how the world/peoples' minds actually work.

Well it makes sense that it can never be perfect.

It's just a little sad in a way

Thats all...